Specifically, we analyzed how people select strategies for counting, and how that selection process is altered by altering task constraints or manipulating the stimuli.

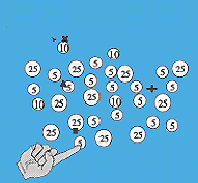
One of our experiments examined how subjects develop strategies for counting coins laid out on a flat surface. Although it is clear that people use a variety of different mental strategies when carrying out such tasks, little is known about the selection, formation, and compilation of those strategies, or how they interact with external strategies for organizing the coins when subjects are allowed to move them around.

Examining this selection process reveals a number of provoking questions concerning how strategies are chosen over a series of trials:

1. Are some strategies measureably better for accurately counting any arrangement of coins, and if so, do subjects learn them?


2. Do pattern/strategy pairs develop, and if so, are they optimal, or simply convenient?


3. Are they cognitively or perceptually driven?


4. Do certain strategies cue other strategies, or do visual/spatial arrangements cue certain strategy combinations?


5. If allowed to use hands as cognitive aids, for counting, remembering, pointing, or blocking out distractors, how does the selection of hand-use strategies affect the selection of counting strategies?


6. How does an imposed time constraint affect the selection of strategies?


7. How aware is the subject of the reasons for his or her selection of a particular strategy?

This simple experiment yielded a surprisingly rich area of investigation, supporting our general belief that our performance on even the most ordinary and common tasks is highly complex and poorly understood. Actions such as coin counting, which appear to involve execution of simple planning and computational algorithims, in fact involve a complex interaction between the subject and the visual environment. Actions taken are highly sensitive to viusal cues, and strategies are selected, altered, and combined "on the fly" based on affordances which present themselves during the accomplishment of the task.

The experiment we designed to qualitatively evaluate subject performance consists of two conditions. We ran pilot studies on both conditions and then focused primarily on the first, with plans to add the second later. In the first condition, subjects were told to sum up the cash value of a number of coins laid out on a flat, white surface without using their hands. In the second condition, subjects were told to count a similar arrangement of coins, but with the added allowance that they could use their hands to help them any way they liked, provided that they didn't move the coins in any way. (We originally included a third condition in which the subjects were given no restrictions at all and allowed to move the coins with their hands. This condition revealed some interesting results concerning efficient vs. inefficient use of space and external representation of information, but the strategies used were entirely of a different sort and used irrespective of differences in the stimuli; therefore this condition was dropped and later run as a separate experiment.)

Since presumably strategies could vary with the number of coins presented, we ran subjects on 25 trials for each condition, with the total number of coins varying from 6 to 30. The coins were either nicklels, dimes, or quarters, represented in close to equal numbers. The procedure was simple; subjects were simply explained the restrictions for the relevant condition, and told to sum up the total cash value of the coins in each trial, and announce the total out loud upon completion of the trial. In each case the time needed to count the coins was recorded along with the stated total, which was later compared with the actual totals to get a accuracy rating for their response. In addition, the subjects were asked to describe their strategies which were subsequently recorded. No feedback was given as to the quality of their performance at any time.

Degrees of inaccuracy were also measured, although not by the size of the difference between the trial totals and the actual totals; accuracy was more appropriately measured by classifying the trial totals according to the actual mistakes made. In most of the cases it was clear how the subject arrived at a mistaken total: figures differing by .05 or .25 were assumed to be due to missing or adding a nickel or quarter; correspondingly, although somewhat less accurately, mistakes of .10 were assumed to be due to dime errors. Errors of 1.00 were assumed to be due to forgetting the accumulated dollar value. Errors of .20 were assumed to be due to mistaking a nickel for a quarter or vice-versa. The above types accounted for 70 percent of all errors; any other errors were attributed either to combinations of the above errors or to mistakes in adding subtotals. The fact that this method of measuring accuracy is obviously not precise enough to draw firm conclusions does not concern us, for two reasons. First of all, the nature of the task is such that the reasons one errs are only of secondary interest. The goal of the task is to get the correct answer; one can be either be correct or not, and degree of error is really irrelevant to the task. The effectiveness of the strategy used must be judged by successful completion of this task, and not by a guess at relative performance; how the errors were made was of interest to us only in examining how different strategies might yield different kinds of errors. Secondly, it is the strategy decisions themselves we are primarily concerned with, and it is part of our hypothesis that relative accuracies of strategies do not influence their selection in this experiment. (Results, in fact, indicate little coorelation between subjects perception of their accuracy and their actual performance.)

The above constitutes the general setup of all the coin counting experiments we ran. Although our goal was to eventually examine how different arrangements might trigger different strategies, it was first necessary to examine the development and selection of strategies for arrangements which varied as little as possible. Therefore in the first control experiment we attempted to hold the variance between the patterns of coins down as much as possible by carefully arranging them in patterns which globally appeared similar (between round and rectangular) and within which the distance between coins was held nearly constant. Care was also taken to prevent coins from lying in clearly delineated rows and/or columns, which would almost certainly cue certain strategies, although this was admittedly difficult. Thus the only significant difference between the patterns of coins in different trials was the actual size of the visual display; 6 coins were presented as a much smaller display than 30 coins.

It could be argued that the difference in display size might have a measureable effect on the speed with which one could process all the stimuli in the visual field, thus confounding the experiment. Therefore, in order to measure the effect of display size (independant of number of coins), I ran a second control experiment. In this experiment, 6 different subjects were asked to count coins as in condition 1, without using their hands in any way. 26 trials were run, in two blocks of 13. During the first 13, patterns were presented randomly with respect to number of coins, which varied as before over the range of 6 to 30. Additionally, the distance between coins for each trial was either great or small, although in both cases constant. In the following 13 trials, the exact same patterns were presented, again in random order, but with the opposite display size: those patterns presented with little space between coins were now presented with more space, and vice versa. In other words, each pattern was presented in an 'expanded' version as well as a 'contracted' version. Following the conclusion of the experiment the accuracy and recorded times were matched to determine whether display size had a significant effect on performance. Results indicate no such effect.

At this point we are prepared to run the first condition as a proper experiment, in which subjects are run on randomly generated patterns which will present features like natural groupings and various irregularities. We will record which strategies are used for which patterns, and the accuracy and times, and attempt to draw some conclusions. A discussion of our expectations follows below.

Two assumptions might be made regarding the strategy selection process. First, one might assume that during the initial trials, subjects would test out a strategy on each trial by making a plan for counting the coins and rigidly applying that plan to a pattern; after which the subject would evaluate his or her performance and make a decision as to whether to continue with that particular strategy based on that performance rating. Secondly, one might assume that during the initial stimuli presentations, the subject would try several different general strategies, and settle on one dominant one to apply to the rest of the patterns.

Our hypothesis is that both of those assumptions are to be rejected. The strategy selection process, is best described neither as a test phase followed by application of the winning strategy, nor even as a test phase followed by the selection of best strategy for a given pattern, on a case by case basis, based on test phase experience. Pilot sudies indicate that subjects do not develop or follow any kind of plan, either in a test phase / application phase sense, or over the course of any single trial. Subjects test new strategies as frequently during later trials as they do in early trials, and individual strategies appear to be composed of sub-strategies which are combined dynamically over the course of individual trials. There is little evidence of planning at all; rather actions are chosen based on affordances that present themselves at 'transitional stages' in the counting process. When presented with an individual pattern, subjects select an initial sub-strategy which only addresses part of the counting task. When the first sub-goal is reached, the stimuli are scanned for affordances suggesting the next sub-strategy to select, the coins already counted serving as distractors. Thus the counting process is seen as a series of sequences of actions (computations) seperated by transitional stages, during which one of several sub-strategies are chosen in a non-predetermined fashion which dictate the next sequence of actions to be taken. Initial and subsequent sub-strategy choices are perceptually driven by features in the patterns.

This can be convincingly argued by the subjects' performance. When a pattern is presented they appear to make an initial decision based on afforded actions. If four quarters are presented together, or two quarters, or two dimes and a nickel, such an arrangement is subitizable and affords mentally separating and counting first as a strategy for starting the task. If no such arrangements are present, the default affordance is to count the quarters, as they are the largest and most visually salient. Although it could be argued that the quarters are often selected first due to the familiarity and ease with which we can count them, that argument is contradicted by the cases in which (for example) the subject starts by counting dimes which by chance form a salient visual pattern such as a crooked row, outliers, or subitizable grouping.

Following the completion of the first sub-goal, evidence for the existence of a transitional phase and use of affordance information in selection the next sub-strategy is often found in comments made by subjects. Commonly subjects start counting without hesitation at the beginning of the trial, but falter and appear uncertain as to how to continue after counting quarters (as if they have difficulty deciding to continue with dimes, or with nickels), making rhetorical comments like "what do I do now?" or expressing gestures of difficulty. Other times, after using the same general strategy several times in a row, the subject switched to an uncommon strategy, with an explanation like " well I just saw that nickel on the side first so I decided to count them first" or " I was counting nickels but I saw those four dimes together so I just added 40 cents on". Also, when subjects count quarters first, they don't follow a consistent continuing pattern for dimes and nickels: sometimes they count dimes first, sometimes nickels, or sometimes both at the same time for reasons seemingly (to both me and the subject) due to irregularities in the patterns. Sometimes subjects describe changing sub-strategies suddenly, after counting only one or two coins. Such evidence argues persuasively for a far more interactive process than medium range planning and algorithmic implementation.

As a final word, it is my intention to run two additional experiments before addressing the second condition. In the first, specific visual patterns will be selected and presented, altered and re-presented in order to show how small changes made in the patterns have predictably high effects on strategy decisions. In addition, it would be interesting to examine the accuracy of the perceptually chosen strategies for the patterns which afforded them. Is it true that the affordances yield optimal strategies, or simply that subjects are saving rescources by not calculating optimal strategies?

As a second experiment, I will run the same trials on elderly subjects to examine how decline in cognitive rescources affects strategy decisions. While the expectation is that there will be little difference in the way the task will be carried out, but significant difference in time and accuracy, there exists the interesting possibility that elderly subjects will [learn to] select strategies according to different criteria in order to compensate for cognitive defecits.