Table of Contents

Abstract

Keywords

Introduction

Complementary Strategies

A Simple Coin Counting Experiment

Complementing Visual Strategies

Memory

Managing Attention

Helping Perception

Conclusion

Acknowledgements

References

Other Articles

Kirsh Home

Formal citation: Complementary Strategies: Why we use our hands when we think. Complementary Strategies: Why we use our hands when we think

Abstract

A complementary strategy can be defined as any organizing activity which recruits external elements to reduce cognitive loads. Typical organizing activities include pointing, arranging the position and orientation of nearby objects, writing things down, manipulating counters, rulers or other artifacts that can encode the state of a process or simplify perception. To illustrate the idea of a complementary strategy, a simple experiment was performed in which subjects were asked to determine the dollar value of collections of coins. In the no-hands condition, subjects were not allowed to touch the coin images or to move their hands in any way. In the hands condition, they were allowed to use their hands and fingers however they liked. Significant improvements in time and number of errors were observed when S's used their hands over when they did not. To explain these facts, a brief account of some commonly observed complementary strategies is presented, and an account of their potential benefits to perception, memory and attention.

Keywords

complementary strategy, memory, attention, perception, cognition

Introduction

A complementary strategy can be defined as any organizing activity which recruits external elements to reduce cognitive loads. The external elements may be our fingers or hands, pencil and paper, movable icons, counters, measuring devices, or other entities in our immediate environment. Typical organizing activities include pointing, arranging the position and orientation of nearby objects, (Kirsh, 95), writing things down, manipulating counters, rulers or other artifacts that can encode the state of a process or simplify perception.

An obvious example of a complementary strategy is using pencil and paper to help add a list of several two and three digit numbers. Most of us find it easier, faster and more reliable to write down incremental sums, and carry overs, than to do the summing entirely in our heads. For long lists, we tend, as well, to recruit the pencil itself as a pointer to help keep our place. Each of these actions has its cognitive benefit. By writing down numbers we offload that portion of working memory required to store intermediate results, by pointing to particular numerals we help direct attention and offload that portion of working memory required to store knowledge of location, and by recording carry overs we set up the environment to simplify verification of our sum, should we desire to redo part of it. In my terminology, such actions complement the internal processes occurring when we add. They are external components in an interactive computation. (Hutchins, 95).

It is certainly no new claim to argue that, as intelligent creatures, we have techniques for altering our environment to enhance our cognitive performance. Cognitive anthropologists, and situated activity theorists have long discussed some of the ways we have of changing our environment to augment cognition. (Lave 88). Typically, however, the changes discussed are cultural, they arise when new technologies are introduced, or when we learn new facts, methods and concepts. They take days or weeks or years to evolve, and they involve sharing resources and frequently cooperating with others. Moreover, they are rarely studied experimentally. (Kirsh & Maglio, 94)

The environmental adaptations I shall focus on, however, occur moment by moment as we manage our workspaces. They are usually quick to set up, and their effect is brief, measured in seconds or fractions of seconds,. Moreover, these strategies are often acquired quickly, as when, for instance, in the course of an activity, we discover the value of pointing, or laying down a ruler, etc. We often learn these by ourselves, and our improved performance can be studied both analytically and experimentally.

In this paper I explore one pervasive example of such complementary strategies: using our hands to help think, remember and perceive. After briefly elaborating the central idea, I introduce a pilot experiment to explore a few of the functions served by pointing and related hand movements. I conclude with a short account of some of the principles underpinning complementary strategies.

Complementary strategies

Imagine being shown an upside down photograph and asked to identify the person depicted. Your natural action is to reach out and turn the picture right side up. Faces are more readily recognized when upright. Apparently, to facilitate perception, we perform an action that adapts the world to our perceptual capacities. This idea -- that sometimes the best way to solve a cognitive problem is by adapting the world rather than adapting oneself -- lies at the heart of complementary strategies.

I believe we learn these adaptational strategies by the thousands. For example, if an agent were given the task of memorizing the letters of a string, such as QIUYOKJHUYTOGU, first without touching the letters, then with touch and re-arrangement allowed, it is likely that he or she would discover a method of moving the letters to reliably increase performance. One such letter-moving technique would be to shift the letters into groupings, such as QIU YOK JHU Y TO GU. Another, more radical technique, would be to re-order the letters in alphabetical order, such as GHIJK OO Q T UUU YY. In any such activity there is a trade-off: the cost in time and effort to perform the complementary activity in the world vs. the time and effort to use existing mental procedures and strategies to accomplish the task without external aid. (Kirsh, 95).

More factors are involved in the choice of a complementary strategy than just speed, however. In addition to (potentially) faster performance the virtue of such strategies is that by changing the local environment -- at the right time and in the right way -- agents are able to reduce the probable error rate, to cope with larger, more complex problems, and to deal with interference more successfully -- all typical measures of performance, and indicators of the cognitive demands a task imposes. Complementary strategies, therefore, allow agents to compensate for resource limitations in working memory and processing power, and cognitive limitations in categorizing skill, and so on. (Backman et al, 92).

The objective of research on complementary strategies is to expose the ubiquity of these strategies -- particularly those that are spontaneously displayed by subjects -- to describe the key trade-offs, such as speed-accuracy, speed-problem size, speed-robustness, and to explain these in terms of an underlying processing account describing the way mental resources are used. If complementary strategies are pervasive, there ought to be general principles governing the shape of trade-off curves for successful complementation strategies.

A Simple Coin Counting Experiment

To observe how complementary strategies enhance performance, a simple pilot experiment was performed. Three male and two female subjects (age 23-38, mean 26) were shown two sets of 30 images, each depicting a different arrangement of quarters, dimes and nickels. Their task was to determine the dollar and cents amount present. See figure 1.

In condition one, the no hands condition, subjects were told not to point at the coin images, or to move their hands. In condition two, the hands condition, they were allowed to use their hands and fingers to point or count. They were instructed to sum the coins as quickly as possible, but to make every effort to give the correct answer. The results showing the mean time taken to announce a sum, hereafter time, and the mean number of mistaken sums, hereafter errors, are given in figure 2. On average subjects took 22.5 sec in no hands and 18.7 sec in hands to announce their answer, and they were mistaken in no hands 68% or 20.3 out of 30 stimuli, (p<.4), and in hands 42% or 12.6 out of 30 stimuli, (p<.4).

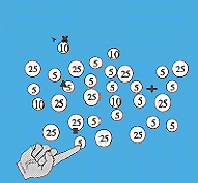	Figure 1. To get a sense of the problem, count the coins depicted in figure 1: first without using your hands and then count them using your fingers and hands. The difficulty in keeping track of which coins one has counted makes pointing a useful complementary strategy. Subjects who have to count real coins can use more powerful complementary strategies such as clustering the coins into denominations, or pushing them off to one side as they are counted. These are familiar complementary strategies which occur naturally. But the experiment reported here did not use real coins or permit physical re-arrangement. The results of the experiment are shown in figure 2.

	Figure 2.

Three features of this simple experiment deserve special mention. First, each subject was tested on a random selection of 30 stimuli in each condition. The number of coins displayed was a random selection of nickels, dimes and quarters totaling anywhere from 21 to 31 coins, (mean of 26), and the number of coins was matched across conditions, so that each subject summed three sets of 21,22 .. 31 coins in no hands (totaling 30 stimuli) and three sets of 21,22 .. 31 coins in hands (totaling 30 stimuli). All S's saw the same 60 stimuli, which were sufficient to yield significant differences in mean error (p < .04) and mean speed (p <.04) for each individual subject.

Second, there was clear evidence that subjects evolved strategies microgenetically. During the first 20% of trials, or so, every subject appeared to be experimenting with different techniques, (this view was confirmed in verbal reports in the debriefing). Later a dominant strategy was selected, and was then used for the rest of the trials in that condition. Once a comfortable strategy was found, subjects usually continued using it even when the condition changed. Thus, when subjects were tested first on no hands, then on hands, the complementary strategy used in hands was geared to help the basic strategy settled on in no hands. Hence the term complementary strategy: performing external actions that complement internal actions. There was verbal support evidence of this pattern of setting a strategy to be used in both conditions even for subjects who were given the hands condition first. These subjects reported trying to count without hands in a manner that resembled the way they had counted with hands.

Third, given the complexity of the phenomena being studied, any claims about what is occurring during the microgenetic phase, and how a complementary strategy comes into being, must be speculative at best. Clearly, subjects are aware of trying out new strategies, both mental and complementary strategies. But we cannot say how they think up new strategies, or why they settle on one strategy rather than continue looking for better ones. Despite this limitation, it is clear that a minimal theory of complementary strategy should provide a set of theoretical principles powerful enough to explain why any particular complementary strategy succeeds or fails in terms of the mental resources and mental strategies used.

Complementing Visual Strategies

In order to evaluate how helpful a complementary strategy is, we must have some idea of the mental strategy it is complementing. The theory of visual routines (Ullman 1985) provides the starting place for a framework for discussing certain mental strategies. It offers an account of the basic computational operations available to a subject for selecting and manipulating elements of a scene, and is therefore a natural place to begin a theory about visually counting. The basic idea is that visual routines are procedures or programs that use primitive visual operations to identify a target property. The flexibility this gives the visual system is that properties invented on the fly, such as a group of four quarters not yet counted, can become targets for systematic visual search.

In Ullman's study there is no explanation of the processes which shape the evolution of visual routines. Nor is there any account of how limitations on non-visual memory constrain the type of visual routines that may exist. The theory of visual routines, accordingly, does not explain how the need to remember intermediate values, such as the dollar value of quarters, or dimes, helps to shape visual strategies for counting. Ultimately, the plan an agent settles on must be responsive to `non-visual' constraints as well. Thus, if the plan is to first count quarters in fours, then add dimes incrementally to the dollar value of quarters, then add nickels, we should see this not as a purely visual strategy, but as a mixed strategy, one that is sensitive both to the visual skills and visual memory limitations of the agent, and the non-visual memory skills and limitations of the agent.

In figure 3 the mixed strategy of subject SR is depicted. Of all subjects, SR displayed the most significant improvement in performance in the two conditions. What is revealing about SR's approach is that his mental strategy regularly called for memory of more visual markers than he could recall. By substituting certain external actions he was able to reduce demands on visual memory enough to reduce errors by 60% and increase speed by 20%. In the debriefing, SR described his strategy like this:

In what follows I will discuss some of the benefits SR reaped with this curious strategy, and tie the discussion to more general notions of memory, perception and attention.

Figure 3a is an attempt to represent SR's no hand or mental strategy. Figure 3b portrays his hand or complementary strategy. The solid triangle, square, circle, cross and X are used to indicate the visual markers proposed by Ullman, and the closed curves mark subitized regions. In 3a, SR has counted all the quarters and is about to start on the dimes. He began his mental counting by subitizing the four quarters in the upper left quadrant and marking the center of that set of 4 quarters with his first visual marker, represented by (. His next step was to subitize a second group of 4 quarters, this time in the upper right quadrant, and mark the set by +. Three quarters remain, all in the lower left, and these he counted and marked with (. Having now found $2.75 worth of quarters he proceeded to `steal' a nickel to make a sum of $2.80, and marked the stolen nickel with his fourth marker (. He then turned his attention to dimes, again beginning in the upper left quadrant. To keep his attention on that location he marked that target with his final marker, X In 3b, SR makes use of his left forefinger to mark the location of the stolen nickel and so to liberate one of the markers for additional use. In his oral account, SR also described using his right hand to help count nickels in twos. But that action is not shown here.

Memory

The most obvious cognitive burden subjects encounter in the counting experiment is to remember intermediate sums. It is easy to drop a digit in counting -- `am I at 285 or 385?' Some subjects' response to this problem was to partially count with their fingers. Subject JD, for instance, would encode the current dollar value on her fingers so that all mental counting could be done using one or two digits. Thus, rather than mentally counting with three digits as in 275, 285, 295, 305, she would extend two fingers and count 75, 85, 95, extend a third finger and count 5. This reduced JD's working memory loads. SR's strategy was equally effective but more baroque. By stealing a nickel to convert odd valued amounts (275) to even ones (280), SR achieved the same economizing in working memory as subject JD did but without reducing digit length. His trick was to limit the phonological complexity of the numeral he had to continually update. The number of syllables kept in the articulatory loop (Baddelly) is greater for two-seventy-five than for two-eighty despite both 275 and 280 being three digits long. Thus, although SR seemed to be using three digit numbers whereas JD seemed to be using two digit numbers, both used equi-syllabic numbers, e.g. twen-ty-se-ven vs. two-se-ven-ty.

Memory savings in syllable length also translate fairly directly into savings in processing time. Presumably, one of the potential limitations on counting speed is the time needed to mentally utter twen-ty-se-ven -- that is, to encode updated sums in articulatory memory. Accordingly, how fast one can count partly depends on the length of time it takes to mentally utter the numbers. Any reduction in syllable size translates to a reduction in counting time. (Baddeley et al, 84). Hence, SR's technique saved both time and memory.

Another savings in working memory produced by SR's technique, stems from shifting items out of working memory to long term memory. SR suggested that his greatest memory savings came from placing his thumb over the stolen nickel, for now he no longer had to remember both whether he had stolen a nickel, and which particular nickel to avoid counting. Prima facie the function of this external marker is to liberate an internal marker. But arguably the real savings lies elsewhere. For presumably, regardless of whether an agent keeps an internal visual marker on a mental representation of a nickel, or an external finger marker on a physical nickel, he still must keep in some portion of memory the meaning of the marker -- here lies the stolen nickel. In the case of internal visual markers, these labels must be in some part of working memory, for the markers are created on the fly with potentially ad hoc meanings. In the case of external marking, however, the meaning of one's thumb on a coin may become conventional, hence drawn from long term memory.

Managing Attention

One easily forgettable feature of attention is that its management is either highly practiced and automatic, or is driven by a program resident in WM. It takes memory to remember the strategy one is currently following. A further consequence of SR's technique of marking the stolen nickel is that it reduces the memory costs associated with running the attentional strategy.

To see this, return to the function achieved by pointing to the stolen nickel. From a purely logical point of view there is no reason to point to one nickel rather than another. The informational function of hiding a nickel is to mark the fact that a nickel, any nickel, has been counted already. This function could equally well be achieved by holding one's nose. But, from SR's oral accounts it was clear that he did not point to a random nickel, and clear, moreover, that when it came time to count nickels, he would intentionally avoid counting the marked nickel. This is not simply idiosyncratic. The action is adaptive. For had SR not hidden a particular nickel, he would be forced to choose a particular nickel to overlook. That is, he would have had to survey all nickels, and recall that his finger being extended meant that one nickel should be ignored. The judgment of which nickel to ignore, however, can be eliminated if a specific nickel is occluded. Accordingly, if SR's finger serves an occluding rather than a marking function, SR will have fewer regions to attend to since he will know which region to ignore. This saves him from following a visual instruction such as, go to that region but ignore the mentally marked nickel. That is, by occluding a nickel, SR is able to reduce the number of distracters he must deal with, and reduce the mental overhead of following an attentional strategy.

Helping Perception

Although pointing and marking can obviously help to direct attention and help to save the use of visual markers, there are several purely perceptual functions they may serve as well. Chief among these is changing the context of observation. In placing one's finger on a surface, the set of items in view is altered. For example, imagine a subject asked to count the following string of dots .................................................... To help fixate on one dot at a time, and reduce the interference from neighboring dots, a subject will naturally want to use a finger or pencil to help keep place. Belying this simple complementary strategy, however, is a sly trick: for by pointing a pencil tip at a dot, and moving it up one dot at a time, one is effectively counting the number of pencil moves, rather than the number of dots. The dots are still too small to count directly, but not too small to touch one by one with an instrument.

Even more compelling is the way adding a feature can alter the static gestalt properties of a figure. For instance, in the Mueller Lyer illusion it is easy to defeat the appearance of unequal lines by placing one's finger over the V portion of one of the lines and visually lining up the tops.

Why do these actions work? How is our visual field affected? An adequate theory of complementary strategy would recruit enough psychophysical theory to explain the mechanism at work, and the likely decrease in error rate.

Conclusion

Intelligent creatures amplify their cognitive abilities by adapting their environments of action to environments where they can get the best results from their limited cognitive resources. A neglected aspect of this adaptive faculty concerns the way hands, fingers and surrounding material objects are recruited for cognitive use. In this paper a simple experiment was presented to show that the performance benefits of such spontaneously created strategies -- complementary strategies -- can be readily measured empirically. To properly understand the basis of these performance improvements, it is necessary to understand the way various external actions fit into an overall strategy of computation. This requires identifying mental functions served by external actions and changes, and enumerating the resources saved in specific cognitive components such as visual memory, articulatory loop, attention and perceptual control. I have done no more than gesture at the range and complexity of these savings here, but the need to explore complementary strategies should be evident.

Acknowledgements

References

Baddeley, A. D. and Lewis, V. J. and Vallar, G. 1984. Exploring the articulatory loop, Quarterly Journal of Experimental Psychology, 36: 233--252.

Backman, Lars, Dixon, Roger A. 1992. Psychological compensation: A theoretical framework. Psychological Bulletin, v112(n2):259-283.

Hutchins, E. 1995. Cognition in the wild,. MIT Press Cambridge, MA,

Kirsh, D. and Maglio, P., 1994. On distinguishing epistemic from pragmatic action, Cognitive Science, 18: 513-549

Kirsh, D., 1995. The intelligent use of space, Artificial Intelligence,

Lave, J. 1988. Cognition in practice, Cambridge, England, Cambridge University Press.

Ullman, S., 1984. Visual routines Cognition, 18: 97-159.