Table of Contents

Abstract

Keywords

Introduction

How to Think About Everyday Activity

Using Space to Simplify Choice

Spatial Arrangements That Simplify Perception

Saving Internal Computation

Conclusion

References

Other Articles

Kirsh Home

This article in a slightly revised form appeared in Artficial Intelligence 1995. Received September 1992. Revised June 1993. Formal citation: The Intelligent Use of Space. The Intelligent Use of Space

Abstract

The objective of this essay is to provide the beginning of a principled classification of some of the ways space is intelligently used. Studies of planning have typically focused on the temporal ordering of action, leaving as unaddressed questions of where to lay down instruments, ingredients, work-in-progress, and the like. But, in having a body, we are spatially located creatures: we must always be facing some direction, have only certain objects in view, be within reach of certain others. How we manage the spatial arrangement of items around us is not an afterthought: it is an integral part of the way we think, plan, and behave. The proposed classification has three main categories: spatial arrangements that simplify choice; spatial arrangements that simplify perception; and spatial dynamics that simplify internal computation. The data for such a classification is drawn from videos of cooking, assembly and packing, everyday observations in supermarkets, workshops and playrooms, and experimental studies of subjects playing Tetris, the computer game. This study, therefore, focuses on interactive processes in the medium and short term: on how agents set up their workplace for particular tasks, and how they continuously manage that workplace.

Keywords

workspace, interactive processes, spatial arrangements, tasks, organization

Introduction

How do we use the space around us? Studies of planning have typically focused on the temporal ordering of action, leaving questions of where to lay down instruments, ingredients, work-in-progress, and the like, as concerns that can be dealt with later. In having a body, we are spatially located creatures: we must always be facing some direction, have only certain objects in view, be within reach of certain others. How we manage the space around us, then, is not an afterthought; it is an integral part of the way we think, plan and behave, a central element in the way we shape the very world that constrains and guides our behavior.

The position I shall defend is that whether we are aware of it or not, we are constantly organizing and re-organizing our workplace to enhance performance. Space is a resource that must be managed, much like time, memory, and energy. When we use space well we can often bring the time and memory demands of our tasks down to workable levels. We can increase the reliability of execution, and the number of jobs we can handle at once. The techniques we use, are not always obvious, nor universal. Some were taught to us, some naturally evolved as we improved our performance through practice, some are inevitable consequences of having the type of bodies, manipulators and sensors we have. In every case, though, the reason space can be used to simplify our cognitive and physical tasks is because of the way we are embedded in the world.

Here is a typical example of using space consciously to improve execution. When preparing an elaborate salad, one subject we videotaped, cut each vegetable into thin slices and laid them out in tidy rows. There was a row of tomatoes, of mushrooms, and of red peppers, each of different length. Our cook then brought over a large elliptical platter -- one she had never used before -- placed it beside the rows and began arranging the items along the circumference. The objective, as was evident from observation and later questioning, was to lay out on the platter all the cut items in a uniform and aesthetic manner. She did not want to run out of tomatoes early, leaving a tomatoless region, or to close the ring of vegetables before all ingredients, peppers, mushrooms, and tomatoes, were used up.

The placement problem our cook faced was to apportion ingredients in a uniform manner. This required either elaborate planning beforehand, recall of similar case experience, or online tracking of the relative number of remaining slices. Having never worked with an elliptical platter this size, our cook had no ready case knowledge to call on. Nor was she eager to count items and measure the circumference of the platter, a step she would perform if planning. Instead she relied on tracking the remaining slices and her moment by moment adaptive skills. To understand why lining up the ingredients in well ordered, neatly separated rows is clever, requires understanding a fact about human psychophysics: estimation of length is easier and more reliable than estimation of area or volume. By using length to encode number she created a cue or signal in the world which she could accurately track. Laying out slices in lines allows more precise judgment of the property relative number remaining than clustering the slices into groups, or piling them up into heaps. Hence because of the way the human perceptual system works, lining up the slices creates an observable property that facilitates execution.

The function of arrangement in this example is to encode, as explicitly as possible, a key piece of information about the problem state. It is easy to analyze how it works. But, in general, how effectively information is encoded in environmental arrangements, depends on the memory, categories, and skills of an agent. There is a substantial literature on memory of chess positions that shows that a single glimpse is enough to allow an expert chess player to remember far more of a game than is acquired by a novice player after many such glimpses. (Chase and Simon, 1973) This suggests that how an expert might store information in arrangements may not be evident to novices. It also suggests that even though we often do not realize that we are structuring our workplace to help us keep track of processes and a host of other useful functions I shall talk about, we should not assume that such cognitive or informational structuring is not taking place all the time. Informational structuring is commonplace.

I doubt that this idea will encounter deep opposition. Yet it has been rarely explored by psychologists. For instance, in a typical psychological experiment about memory, experimentalists set out to test a conjecture by systematically altering properties of the stimulus and observing the effect on certain dimensions of performance, such as how much, how reliably, how fast the stimulus material is remembered in free recall tests, in cued recall tests, or in recognition tests. Such tests are supposed to tell us something about how the agent organizes the stimulus material internally. Thus, the reason the string KXTNJQXTARWOYE is less memorable than the string IBMCIANBCDARPA is that it cannot be broken into known strings. After a while, many subjects (depending on background) will chunk IBMCIANBCDARPA into four more easily remembered strings IBM CIA NBC DARPA. Agents project structure onto the world. But curiously, experimentalists rarely allow the subject to play with the stimulus itself to highlight the chunks, as we note in scrabble. They do not set up experiments to determine how agents choose to structure the stimulus.

The tendency to delay study of the cognitive/computational virtues of spatial arrangement is not confined to psychology. Consider the following blocks world problem so fondly studied in planning. A child is asked to build two towers out of lettered blocks so that the first tower reads SPACE and the second reads MATTERS, as shown in figure 1. The blocks are currently scattered around the room. If we assume that standard AI blocks restrictions apply then only one block can be moved at a time, and only if there is no block on top of it. How shall the robot proceed? One method never discussed in the AI literature is to preprocess the blocks so that they spell out the goal stacks SPACE MATTERS horizontally on the ground.

	Figure 1.

Why might this be a good idea? Because it serves as a proof that there exists a goal linearization that will work. If we can build SPACE MATTERS horizontally we know we can build it vertically. We can guarantee construction. At first this may not seem to be an advance over simply building the towers directly. The benefits of informationally structuring the world do not appear to be worth the effort. But if we factor in that the constraints on horizontal movement are weaker than those on vertical stacking, we can see that to solve the problem on the ground is to solve the problem in a more abstract space. On the ground, we can pick up and move a block regardless of whether it is sandwiched between blocks. And if we leave space between blocks we can insert a block without first shifting the others around. Hence, we can save many steps by solving the problem on the ground first, since if there is going to be external trial and error search in finding the goal ordering, there are far fewer moves to make on the ground. It is easier to solve the problem on the ground.

Such exploitation of the world to improve execution, or to simplify problem solving, is typical of situated reasoning. In a host of studies, (Scribner 1986, Lave 1988, Greeno 1989), it has been repeatedly shown how human agents make use of resources in the situation to help draw conclusions and solve problems rather than use abstract, symbolic computations. People make mental tools of things in the environment. Lave (1977) emphasized the ubiquity of specialized "environmental calculating devices". For instance, in a famous example (de la Rocha 1985), cited by Greeno (ibid.), an interviewer asked a subject who had recently enrolled in the Weight Watchers diet program, "How much cottage cheese would you have if you served three-fourths of the day's allotment, which is two-thirds of a cup?" After the man muttered that he had studied calculus in college, he measured two thirds of a cup of a cottage cheese, put it on the counter, shaped it into a circle, put a horizontal and a vertical line through it, set aside one of the quadrants, and served the rest. Instead of multiplying 3/4 X 2/3 = 1/2, he used objects available in the situation to solve his problem.

Now space is always present, and the need to place objects somewhere is a constant fact of life. This makes space an invaluable resource to exploit in order to facilitate everyday problem solving and planning.

My goal in what follows is to provide the beginning of a principled classification of some of the ways space is intelligently used. The data for such a classification is drawn from videos of cooking, assembly and packing, everyday observations in supermarkets, workshops and playrooms, and experimental studies of subjects playing Tetris, the computer game.

The remainder of the paper is divided into five parts. In the first, I introduce the general framework within which to think of intelligence and space. Our use of space is not a special case of intelligent activity which somehow deviates from our normal methods of interaction; the way to understand how we exploit spatial resources is part of a more general approach to the study of intelligent activity. In the next three parts, I present my classification organized into:

In the final part I draw some conclusions.

How To think about Everyday Activity

The approach I shall be endorsing falls squarely in the interactionist camp: to understand human behavior, and to design robots that scale up to complex dynamic environments, we must explore the interaction between agent and environment. Humans, to a significant degree, shape and even create the environment, that in turn, influences their behavior and development. We can study this interactive process along different time scales. As Hammond et al, (this journal) have done, we can study the way agents restore the environment to states which they (the agents) have methods to deal with, thereby diminishing uncertainty, reducing the number of contingencies that have to be built into programs, and allowing streamlining of plans because agents can rely on things being as they ought to be, more or less. The stabilizing processes Hammond discusses, are long term stabilizations.

But, equally, we can study interactive processes in the medium and short term -- as I shall be doing here. For instance, we can study how agents set up their workplace for particular tasks, and how they continuously manage that workplace. To take an example, an agent who knows he will be acting as a short order cook may equip and maintain his kitchen with implements and standard resources that regularly are required -- i.e. long term structuring. But, on being given a particular order, say, a mushroom omelet, hash browns and whole wheat toast, the cook must still prepare the workplace specifically for that task -- laying out the eggs, the cut mushrooms, and the requested number of pieces of bread. In setting up the workplace for the particular task the cook arranges items so that the amount of work that has to be done in the high tempo phases of the cooking of this particular dish is both simplified and reduced. This readying of the workplace is a medium term structuring of the environment.

Short term structurings arise when ingredients and implements are deployed adaptively in the cognitively demanding phase. Once the task has entered the main phase, we find that agents, particularly expert agents, constantly re-arrange items to make it easy to:

To return to the diner, if several orders are being prepared, we have observed short order cooks, clustering the materials for orders together, and leaving knives, forks or other utensils near the ingredient to be used next, as if to mark their place in their plan.

Throughout this paper, I shall be operating with several assumptions it is best to make explicit. These have been instrumental in shaping the interpretations of behavior I shall be offering.

Of these four tenets, number 3. -- ways of informational structuring -- will be my primary focus. It is worth elaborating numbers 2 and 4, as well, however, to get a proper perspective on this approach to embodied everyday activity. Readers who are impatient to see the classification of ways of using space intelligently may skip to Section 3.

Experts don't plan much.

The hallmark of expertise, from a behavioral standpoint, is effectiveness and robustness. The hallmark of expertise, from a theoretical standpoint, is sufficient compiled knowledge to cope with normal contingencies without much on-line planning. A major factor in this compilation is expert perception: having the right perceptual categories, and knowing how to keep an eye on salient properties. [Chase and Simon 73]. It is widely accepted that, for experts, there is tremendous local constraint on what should be done next. (Charness 1981). Practice has tuned the perceptual systems of experts, both to the microfeatures and cues that correlate with effective action [Agre & Chapman 87, Brooks 91, Kirsh 91], and to the conditions when it is most helpful to attend to those cues.

Rasmussen [1980, 1986] and Reason [1990] have elaborated this viewpoint in some detail. On their account, once an expert has decided what its goals are -- what to cook for dinner, for example -- the majority of activity that follows will be under what they call, skill-based and rule-based control. [see also Rouse 1981, Norman 1981, Reason 1990, cf. Agre forthcoming]. These control structures, it is thought, are extremely responsive to current environmental conditions.

In the case of skills, this responsiveness is automatic and unreflective. When we make ourselves a cup of tea in our home kitchen, for example, we 'automatically' comply with the orientation of faucet, kettle, cups, the water pressure, automatically retrieve the tea bag, milk, teapot, and so on. These actions are unreflective in the way habits are unreflective. That is, the actions are intentional, but not the product of occurrent deliberation.

In the case of rules, this responsiveness is also largely unreflective and automatic, triggered by perceived state information, but a rule has been invoked because the agent is aware that something unanticipated has occurred, that skill based behaviors are beginning to drive things off course, and that corrective measures need to be taken. Thus, the need for a rule based response will be triggered by one of the attentional checks on behavior that are part of skill-based activity. Once a disruption is noticed, the corrective action to be performed is determined by a rule in one of the `problem-solving packets' an expert has. For example, in the course of serving tea if we discover a dirty spoon, in normal circumstances, we will unreflectively wipe it clean, or reach into the drawer for another, or do whatever is obvious to put the process back on track. Even routine activities in familiar environments constantly give rise to such simple problems. For most of these problems, it is suggested [ibid. Rasmussen], experts find sufficient cues in the situation to trigger a known rule without halting the activity in order to consciously and analytically take stock of the situation and reason or deliberate about a solution.

Conscious analytical processing -- deliberation, as I have been calling it -- is required when things begin to get too far out of control to rely on existing packets of problem-solving rules to manage the process. Only then must the agent consider non-local facts and goals, in order to formulate a plan to bring things back on track, or to find a new path to the goal. Most expert activity is locally driven.

Experts jig their environment.

There are two obvious ways experts can increase the percentage of time spent operating in skill and rule based modes. The first is to broaden the range of cases the skills and rules cover, thereby learning how to automatically cope with more diverse and uncertain environments. The second is to build into those skills and rules an environmental dampening factor that tends to decrease the variability of the environment. This is the force of tenet three -- experts partially jig the environment as they go along. It is here that space becomes of paramount importance. Let me elaborate.

A jig is a device for stabilizing a process: it is a mechanism for reducing the degrees of freedom of a target object. A vice is a jig, a table top can serve as a jig, but so can a `pick' in basketball, or the slides on a cabinet drawer which determine the direction of free movement, or compliance. Jigging is one way of preparing or structuring the environment. The more completely prepared an environment is, the easier it is to accomplish one's task.

We can draw a logical distinction between physically jigging an environment and informationally jigging it; although in practice the two often go together. The distinction is between planting information in the environment to reduce the perceived degrees of freedom, and planting physical impediments or constraints in the environment to reduce the physical degrees of freedom an agent actually has. At the simplest level, the difference is between cues and constraints. In informationally jigging an environment an agent will usually arrange items (consciously or sometimes unconsciously) to draw attention, to cue cognitive events or processes in himself or herself, or another agent. For instance, in supermarkets, store managers succeed in biasing consumer choice by having large displays of 'specials' at the head of isles, by putting up flashy signs, by expanding the length of store shelf devoted to certain brands, and the like. These tricks alter a shopper's perceived choices, but do not actually restrict the range of physically possible actions. In physically jigging an environment, however, an agent arranges items (consciously or sometimes unconsciously) to physically constrain action. Thus, sticking a door jam under a door serves to constrain the physical freedom of an agent. If the agent can be counted on to notice the jam, then it can also be relied on to serve as a cue, an informational jig, but there are many cases where the physical constraint goes unnoticed, and so acts as a physical jig alone.

I shall be concerned primarily with ways of arranging items to informationally jig the environment. As suggested, these include a variety of cueing techniques, but are not confined to those. For instance, the set of actions perceived possible may be reduced by hiding or partially occluding objects. Pull down menus that display only some of the options available in a situation, is one such example. Another is found in the practice of dieters who keep certain foods in the pantry and out of the fridge, to prevent snacking. Out of sight is out of mind. Here, arrangements serve to constrain rather than cue perception.

Nonetheless, cueing is the key method of informationally structuring an environment. Agents 'seed' the environment with attention getting objects or structures. These can be harnessed to not only reduce perceived choice but to bias the order in which actions are undertaken. When I put a roll of film by the doorway, for example, I am using space to create a reminder to prevent me from just marching out the door without remembering my earlier intention to get the film developed today. Reminders usually rely on attention getting elements to draw our notice. For instance, contextually unusual features, such as a surprising color, or an unexpected sound or smell, will often prompt reflection; as will being in just the right place at the time to be useful in a task. Such features work because we have sufficient knowledge of our tasks and plans that when, in the course of activity, we notice these felicitous events, or surprises, we are reminded of aspects of our tasks that must be performed. If successful, they capture our attention at the right time and alert us to opportunities we might have missed, or they reduce the likelihood of performing a so-called `double-capture slip' . These are slips arising from failure to notice a relevant choice, or change in circumstances, with the effect that a "frequently done activity suddenly takes charge instead of (captures) the intended one". [Norman 1988, p107].

Much of what I shall present in the following sections concerns ways of using spatial arrangements to informationally jig or structure the environment, and much of that focuses on ways of keeping attention properly directed. It is worth noting how environments that are dedicated to certain tasks already incorporate some of these ideas. This is the point of stressing tenet four: that most task environments are pre-structured.

Pre-structured environments.

Let us say that an environment E, is well designed for a particular task T, and a particular agent A endowed with skills S, and rules R, if, at every choice point, the environment provides sufficient physical and informational resources to locally determine A's choices. On the one hand, this will require E to be rich in task useful physical structures, for instance, E ought to have tools and surfaces which make it simple to satisfy regularly recurring preconditions in T. Thus, for cooking, where many tasks involve chopping, cutting, or slicing, we find kitchens equipped with knives in convenient reach, and hard flat surfaces -- two obvious preconditions for most cutting-like actions. On the other hand, a well designed environment will also have to be rich in useful informational structures --- cues and the like -- to make it simple to cope with the cognitive demands of the task. For example, in most kitchens [Agre & Horswill 92], there are also timers, thermometers, oven lights and, of course, temperature settings to help us to see where in the process we are, and what must be done next. These devices populate the world with readily available task relevant properties. Lids rattle when pressure builds up, kettles whistle or turn off automatically.

The distinction we introduced before between a purely informational jig or structure, and a purely physical structure, can be made more rigorous as follows. An action that structures the environment in a purely informational way achieves nothing that could not equally well be achieved by asking an oracle. This contrasts with actions that structure the environment physically, which reduce the physical complexity of a task by satisfying either preconditions or background conditions of actions.

This is worth explaining. An oracle is a device that can answer in unit time any instance of a particular decision problem. We might ask an oracle 'what should I do next, given my current situation and goals?' Or 'What are the likely effects of performing this action in this context?' Or even 'What is the current state of the environment?' If the question asked is well-posed, i.e. decidable, the oracle will `instantly' return the correct answer. Oracles save computation. But they cannot save physical execution. Oracles can't slice or fry an egg; they never bring an agent physically closer to its goals.

For instance, to return to our blocks world example earlier, imagine we are dealing with blocks in which each block is lettered on one face only. As before, the goal assigned the planner is to build a stack in which the letters form two sequences SPACE MATTERS, but, this time, the letters can be in any orientation. If not all the letters are visible, some of the blocks will have to be turned over before the stack can be built so that we know we are building the towers with the right ordering. These external epistemic actions would not be necessary if we had an oracle or a partner in a better position to tell us a block's letter. The interesting thing is that the action of re-orienting a block does not satisfy any physical precondition of the goal. The goal, as specified, allows the agent to place blocks without concern for direction. Accordingly, such actions are pragmatically superfluous. They are broadly equivalent to placing an oracle in the environment which is able to remind us where each block is as soon as we ask (look).

Self-adjusting data structures provide a more formal model of the benefits of informational structuring. A data structure is self adjusting if each time an element is inserted or deleted, the structure executes an adjustment routine which performs simple changes to maintain certain 'nice' properties. For example, in many sorting problems where binary trees are used to store the elements, it is possible that, due to some sequence of insertions and deletions the tree will become thin and long. Although traversing such a tree in left hand traversal is a linear time procedure, the process of deciding where to place the next element -- that is, constructing the tree -- is quadratic. If, however, certain small local changes are made to the tree whenever an operation is performed on it, we can guarantee keeping the tree wide and short. By incorporating such a scheme into the construction phase of our tree sorting algorithm we can improve performance, yielding an O(NlogN) algorithm.

Now the idea of making local changes in a data structure as we go along in order to improve performance is very much like making small rearrangements to the position of objects in our workspace to help us to find objects, to highlight change, or to allow us to use more efficient or familiar techniques. Both cases, self-adjusting data structures and reorganizing of the workspace, would be otiose if we had an oracle to advise us on what we must do next, or on where a particular element is to be found.

The implication is that rearrangements may be done just as much to make objects convenient mentally as to make them convenient physically. Restructuring is just as likely to serve a cognitive function: to reduce the cost of visual search, to make it easier to notice, identify and remember items, and, of course, to simplify one's representation of the task.

A word about complexity analysis.

Although I have been arguing that the point of informationally structuring space is to reduce the time and memory requirements of cognition, the actual reduction in computation achieved by the various methods I shall discuss does not, in general, lend itself to meaningful quantitative estimation.

For instance, from a classical information processing point of view, choice is the outcome of a heuristic search of options represented in a problem space. The problem space lays out decision points, feasible actions, and some fraction of the consequences of taking choices, and the agent relies on various heuristic methods to discover a goal path. The main ways to reduce the complexity of choice, then, are to revise the problem space so as to:

Other ways of reducing the complexity of choice are to:

Working within such a framework, it ought to be possible to determine, for any given problem, what is the expected computational savings of an improvement in one of these ways. Because there are external counterparts to most of these ways we would expect it possible to generate similar complexity analyses. It should not matter whether the change in the agent's computational task comes from modifying the world to simplify choice, or modifying the internal representation of the world to simplify choice. Yet, in practice, the analyses have limited significance.

For instance, in figure 2a we see a graphical representation of the value of having heuristics. Theoretically, an agent who modifies the description of state to allow application of a heuristic powerful enough to single out a unique action at each choice point, can reduce the complexity of search exponentially, from bn to n, where n is the average depth to the goal node and b is the average branching factor. The agent can just choose the best action at each choice point without checking for downstream consequences. Yet how many agents actually search through all the steps in a plan before choosing the first step?

	Figure 2.

The external counterpart to method 3 -- modifying the description of problem state -- is to add new `heuristic cues' to the workplace. For example, in the salad making case mentioned in the introduction, we might argue that lining up the vegetables not only helped determine the value of the cue `relative number remaining', it altered the environment so that the heuristic based on it was now usable. To realistically calculate the savings of such a cue, however, we would like a cost-benefit analysis comparing the time lost by physically lining up the items, versus the savings in improved layout performance. Empirical experiments can be done. But these hardly count as formal results. They certainly will not tell us much about the internal computation saved, since different agents who use different methods will have tricks and shortcuts too, thereby frustrating appealing to empirical findings for worst case results. What is interesting about the examples, then, is not how much they reduce computation -- for that we cannot meaningfully estimate -- but how easily they reduce it.

Using Space To Simplify Choice

Cues and Constraints.

Prima Facie, choice is the product of search -- visual search for the actions that are currently available, and mental search of the desirability of those available actions. Arrangements which reduce either type of search, simplify the computational burden of agents. In figure 2. there is a graph theoretic portrait of three ways search can be so reduced. Information via cues and constraints can be added to a problem in order to:

Reducing Perceived Actions

To see an action as available for choice is to notice that it is afforded by the current situation. An affordance of a situation, crudely stated, is a way that a situation lends itself to being used. [Gibson 77]. An empty container affords filling, an active television affords viewing, and a hammer affords striking. Because of the relational nature of affordances, we need to tie them to the action repertoire of an agent. A television does not afford viewing to a blind person; a hammer does not afford hitting to a creature without manipulators. A situation has an affordance for a particular agent. Moreover, we can change the affordances of an object merely by altering its context. A television does not afford viewing when enclosed in a box; a cup does not afford filling in a liquidless environment. An affordance, as we shall use the term then, is a dispositional property of a situation defined by a set of objects organized in a set arrangement, relativized to the action repertoire of a given agent. Agents perceive an affordance, when they register that one of their possible actions is feasible in a situation.

Because an agent need not register all the actions feasible in a situation, the action set which is perceived as feasible (the perceived action set) is sensitive to properties of the situation, particularly arrangement. Two general ways of biasing the perceived action set are by:

Clever placements do both, often at once.

Case 1: Production Lines Hide Affordances

Production lines have been around long before Henry Ford. Every time we serially decompose a complex task by dividing the space in which it is performed into functional stations where specific subtasks are performed, we create a production line. Of course, Ford added the notion of pipe-lining. But the principle is the same: by regionalizing subtasks we restrict the kind of actions an agent will consider undertaking. Only certain inputs find their way into each region, only certain tools are present, and so only certain actions are afforded. We may think of each spatial region as creating a task context, or task frame in which only certain skills and rules are appropriate. This has the effect of decreasing the fan out of perceived options and eliminates the need to memorize anything more than the most abstract steps in a plan.

For example, in my kitchen at home, a task as simple as preparing a plain garden salad, reveals a latent production line because I wash vegetables by the sink and cut them on a chopping board. More precisely,

When we examine this task we note two uses of space:

The equipment and surfaces of a station effectively trigger an action frame or task context in which only a fraction of all actions are considered. Once a context of action has been triggered, the local affordances make clear what can and must be done. If a tomato were viewed in isolation, a cook in search of a salad might consider chopping it, washing it, placing it directly in a salad bowl or plate, or even eating it on the spot. To perform most of these tasks the cook would have to first find the relevant equipment -- knives, sink, bowl etc. Exactly which task the cook would do would depend on where in the plan he was. The virtue of spatially decomposing the task is that one need not have to consult a plan, except at the very highest level, to know what to do. Each task context affords only certain possibilities for action. You don't think of washing vegetables when they are sitting beside a knife and a cutting board, unless their unwashed state stands out and alerts you to a problem. Similarly, if an item is unwet and beside the sink, for all intents and purposes, it carries a `wash me' label. A cook entering the room can read off what is to be done, for there is enough information available in the set-up. The reason production line layouts are examples of hiding affordances rather than highlighting affordances is that the context of action delimits the range of immediately available actions to the ones that are `ready to go'. When a knife and board are present, cutting actions are ready to go, and washing is not.

	Figure 3. In this figure we see a typical kitchen with its stations for chopping, using the burners, baking, and cleaning up. In professional kitchens separate staff may operate these stations, but in household kitchens, the same agent moves from station to station, often carrying tools along as he or she moves. The equipment and surfaces of a station effectively trigger an action frame or task context in which only a fraction of all actions are `live' options. This reduces the complexity of choice by creating a production line. A production line works successfully when a global task can be spatially decomposed into subtasks where the output of each subtask is a suitable input to the next subtask. This has the effect of decreasing the fan out of perceived options, and eliminates the need to memorize a plan.

Case 2: Cueing Blocked Actions

Production lines that prevent workers from moving around to where tools are kept, create a set of dedicated workers. Actions are therefore not merely out of mind, they are out of bounds. In household kitchens, though, the same person does many tasks; stations are not fixed and tools move around. This means that although we have action frames, or task contexts, which have the effect of dropping from our sight certain actions that, though not available locally, are still available in principle, we aren't physically or socially unable to perform those out of context actions. Such actions become impossible only when something in the environment restricts the physical freedom of the agent. For instance, by putting a door jam under a swing door, one of the directions of opening can be blocked. One is free to open the door, but not to open it in the blocked direction. That action is physically unavailable. This practice of changing the task environment to eliminate degrees of freedom we call blocking.

Blocking usually restricts affordances by changing the action context so that certain preconditions are clobbered. This is seldom a permanent change -- the door jam can be removed. But often the change is meant to be noticed; it signals the fact that a precondition has been intentionally clobbered. Some spatial arrangements say `Don't do X.' They cue a prohibition.

Here is a second example.

As is obvious from the examples, the physical context has not been irreversibly changed. An agent could undo a blocked precondition, in the same way that an agent could take a knife out of the drawer to cut a tomato. But, the distinction present is that a rag on a pipe, or a plug in a sink, are not just physical impediments to action; in most cases, they are intentional, meaningful cues. A visible wedge, a clamp, a boot on a car, a club on the steering wheel, a blockade, are further cases where knowledge of how a device functions can be counted on to make these physical impediments salient. In principle, any easy to notice clobbered precondition can be harnessed to signify that a particular path is obstructed, irregular, contaminated, or otherwise blocked. But the most reliable will rely on 'natural mappings'.[Norman 88] and will themselves satisfy the psychological conditions of being good cues. Thus, the absence of a knife, is a less good cue than the presence of a pair of oven mitts. That being said, a convention can be set up whereby almost any arrangement can be called into service to signal prohibition. For instance, a completely set table marks its being prepared for something special: other activities that are regularly performed on tables, such as writing, drinking tea, etc., are outlawed.

Case 3: Arrangements that Draw Attention to Affordances

We have seen two ways of reducing an agent's perceived option set by structuring the workplace. The first eliminates actions from the perceived set by reducing affordances so that certain actions are not perceived as locally available, the second eliminates certain actions from consideration by prohibiting them -- by creating cues that carry the message don't do that. Examples of arrangements created to steal attention -- to highlight affordances -- are not as straightforward. But they are prevalent.

We can distinguish two sorts:

The difference between the two turns on how habitual the action is that is cued. For instance, at the check-out counter of supermarkets the person bagging groceries operates in a strongly skill-driven manner. Owing to their accumulated knowledge about the items that must be packed, and the space available for buffering, baggers build up regular ways of solving their bin packing problems. Among their other tricks, they rely on arrangements in the buffer zone to help call attention to obvious properties of the inventory.

Grocery packing is a complex interactive process in which control oscillates between being internally goal directed -- `I need an intermediate object now'-- and being feedback or data controlled -- `can't I put this item in one of the bags I've started already?' By partitioning the space into identifiable clusters -- `I need a heavy object -- there's a bunch by the register'-- the agent reduces the complexity of choice. This works in several ways. First, by creating equivalence classes of items, heavy, intermediate, fragile, small, the bagger makes it easier to spot a sought after type of item, and also easier to grab an item of that kind in a hurry. Three small items clustered together make it easier both to remember and to see where a small item is. Second, the urgency with which an item of a certain kind need be packed correlates nicely with the size of its build-up in the buffer zone. Because size is an attention getting feature, the largest pile cries out for early use. This has the salutary effect that the agent is less likely to forget items in larger piles, and so, other things being equal, is more likely to use an item from that pile next. Third, items nearer to the center of the workplace, are more likely to get noticed as vision sweeps over them in the normal course of packing. Hence, other things equal, they too have a greater likelihood of being used. It is not surprising that on questioning, baggers admit to often reserving that space for items they intend to use immediately after the next item. In each case, then, placement of items serves to highlight particular features that are useful. Clustering highlights the functional category of items; size highlights urgency; and centrality highlights what is next to be used. Each highlighted feature helps to bias choice.

The second class of attention related biases relies on setting up the environment to increase the chance of noticing regularly unnoticed possibilities -- of seeding opportunities. It is remarkably prevalent. Almost every activity produces by-products and side effects, some of which can be re-used. For instance, in repairing an old car the nuts and bolts removed when replacing a worn out part are rarely thrown out immediately because they may prove useful later in bolting the new part in place, or in other repairs. 'Don't throw out what might be useful' is a conservative but rational policy. Yet there is a trade-off. The more that is retained the more cluttered the space, with the result that the very opportunities that might be found go unnoticed. How do agents manage task detritus?

	Figure 4. A typical check out scene in a supermarket reveals seeding the space around one with attention getting clusters of goods. Skilled baggers build buffer zones that collect as yet unpacked items in functional groups such as fragile, heavy, keep upright. The groups of items that are nearby are likely to be used sooner than items more distant. The purpose of the groupings appears to be that of enhancing the affordances of the items. Thus heavy items afford support, hard items afford protection and so on. As baggers learn how to buffer and manage the space around the register better they begin to pack faster and more effectively. Not only do they have what they need more at hand, they can see what they have and so simplify choice.

The principle behind clever by-product management is to leave around whatever has a good chance of promoting opportunism. Opportunism is the practice of taking advantage of opportunities the environment provides in order to fulfill a goal one did not originally set out to attain -- the opportunistic goal lies outside one's current sub-goal context. Moreover, it is important that the cost to attain the opportunistic goal is lower than normal -- the context provides the agent with a golden opportunity.

A simple example of cultivated opportunism is found in the practice of carpenters.

By wisely leaving around a certain clutter, an agent multiplies the chances of getting something for nothing. But not just anywhere will do. The most successful ways of seeding the environment seem to require placing objects in positions which have the greatest chance of displaying their affordances. This is not always easy, for given the number of affordances an object has, it seems to require knowing which affordances are going to be useful, when they are going to be useful, and how to lay them about to call attention to just those affordances. Thus, the problem of facilitating opportunism is to find a way of leaving equipment, intermediate products, and task detritus around the workplace to highlight particular affordances.

If the agent has a system for placing objects -- 'I always keep the useful scraps over there' -- their affordance will be known. But equally, if clusters of objects, organized by affordance, are built on the fly the agent also has a better chance of noticing opportunities. A clear example shows up in flower arranging.

In general, cueing attention to bias choice is a hit or miss affair. But, given a clear understanding of what cues stand out, and how agents can encode meaningful pointers out of them, we might hope to build systems for exploiting cues to reduce task complexity.

Eliminating Decisions

	Figure 5.

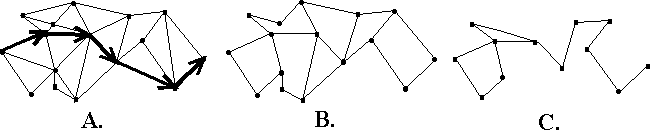
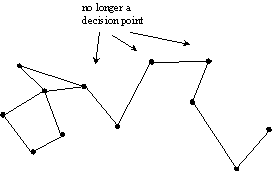
Let us say that a decision has been eliminated altogether if an agent has no choices to make when at that state. A state may be at the meeting place of several actions fanning in, or there may be only one previous state leading to it. In either case, if a state has no fan out, we shall say that it no longer marks a decision point. See fig 5.

Good designers are forever looking for ways of contracting the number of decisions users must make: not just in the number of actions they must consider at any point but in the number of times they must make a decision at all. The fewer degrees of freedom an agent has the simpler its task, providing of course that the outcome is what the agent wants. Ultimate simplicity comes when there is only one degree of freedom, or, more realistically, many degrees at the outset of a task, but then after that none: the outcome is ballistically determined. It is forced.

Most examples of informationally forced choices are limiting cases of blocking, narrowed action contexts, or attention stealing. Here is a different case that shows how properties of our three dimensional topology can be exploited to simplify a problem, and so, in effect, do away with earlier choice points.

The key technique in eliminating decisions shown here is to substitute compliance for choice. Once the tailor has laid out the tracing paper, the rest is ballistic. There is no need to make moment by moment decisions about where to position the scissors: it is to follow the chalked line. Nor, for that matter, is it necessary to explicitly calculate the mirror image paper mock-up. The simple flip transform achieves that. By exploiting topological properties of the action space, certain otherwise key decision steps in trouser construction have been designed out of the process. The layout and cutout processes are now so streamlined, and constrained, that there is no real choice.

Offloading Heuristic Properties

The third, and final way of using space to simplify choice is by creating arrangements that serve as heuristic cues that indicate the desirability of actions.

Let us understand a heuristic property to be an easily computed property of a local situation which allows us to rank the desirability of available actions. In rational decision theory, heuristics (or case knowledge) are supposed to serve as a plausibility filter, to be activated after a filter for availability has been applied. (Elster 82). Heuristic information is supposed to explain how live options can be ranked on the basis of local information. The distinction between this type of local information and the type of local information available in cues that prohibit, draw attention, or remind, is not hard and fast, but can be made by examining the scope of the information. A heuristic cue, unlike a plug left on the drain, normally applies to many choice points. For instance, in lining vegetables up into rows, our salad maker created a heuristic cue that was meant to apply repeatedly to decisions over the course of the task. It was a way of setting up the world to key into the skills of the agent over the long haul. Accordingly, the set-up costs could be amortized over the whole task. By contrast, in leaving a plug in the sink, or in placing the next item to be bagged close by, the cost of set-up must be paid off by the savings in the next few actions

Case 4: Encoding The Temporal Order of Actions

One of the most obvious and compelling ways of using space -- and judging by conversation, the one most likely to leap to mind -- is to lay down items for assembly, in the order in which they are to be put together, touched, handed off, or otherwise used. Space naturally encodes linear orders, and higher orders if the agent has a system. The obvious virtue of encoding orderings in the world is to offload memory. If I can arrange items to display the sequence they are to be used in, then I don't have to remember that order, or figure it out, or consult the manual, as long as I know how to read the information off the local properties of the world.

Let us view an assembly problem as having two components: the selection problem -- which piece is the one to attach next; and the placement problem -- where and in what orientation should it be attached.

Here is an example of arranging pieces to simplify the selection problem.

Computationally, the advantage of having an ordering is obvious. In the extreme case, we reduce a doubly exponential problem of deciding which piece to select and where to place it, into an exponential problem, since the selection problem is essentially solved. To see this, suppose the placement problem is regular: that, at any moment, there are only two possible places a piece can fit, front or back of the assembly. If the agent knows the right ordering, and hence has a solution to the selection problem, then since there are two possible placements for each piece in an arrangement, there are, in the worst case, 2ⁿ possibilities to search through. If the agent must solve both the selection and placement problems, simultaneously then all n permutations of placements must be considered, generating O(2²ⁿ) possibilities to test. In the felicitous case, where the assembly forces a unique placement, and there is only one place a piece can fit at any moment, then given the right ordering the assembly problem is constant time. By contrast if the agent must find an ordering, the problem is O(n²), even when the assembly forces a unique placement, because at each step the agent must try out the remaining pieces.

The trick in using space to encode placement order is obviously to have an ordering that is easy to read off an arrangement. Intuitively, linear orderings are just such an arrangement; they have a natural meaning for next. Moreover, arranging parts linearly, has the added virtue that it is hard to misplace items. If all parts are in a line, you know where to look. No surprise, then, that straight line orders are commonplace. But there is a danger, too, in using linear orders: the longer the line of pieces, the more likely the pieces are to be kicked out of order. Consequently, for the sake of robustness, assemblies involving many parts are better placed in a compact group. And indeed anecdotal reports suggest that small groups are popular: bolts and nuts clustered together, sub-assemblies off to a side. Furthermore, a simple linear order is not an expressive enough structure to carry information of the form: build sub-assemblies one and two first, then assemble those sub-assemblies, then assemble sub-assemblies three and four. (See figure 6.)

As arrangements become more complex, however, they lose much of their naturalness of interpretation, and depend more on an agent's ability to remember how things were laid out at set-up time. Memory for location is a current topic of psychological inquiry. In an early discussion of this topic, Malone (83), provided anecdotal evidence that subjects are surprisingly ept at locating documents in their office space. This was thought to reveal hidden virtues in messy desks, for the messier the desk, the more categories and cross references one can achieve --at least, in principle. In a more recent study of locational recall, though, Lansdale [Lansdale 91, p1172.] suggests that a subject's ability to recall the location of an object -- a computer icon in an array -- is disappointing in comparison to Malone's anecdotal evidence. ' The reason the subjects themselves most often offered for their poor performance -- as revealed by their most frequent complaint during the experiment --was that `the different locations were arbitrary: there was no meaning to them, and hence the encoding of locational information was an abstract process.' [Lansdale 91 p 1174] Further experiments which allowed subjects to exploit an encoding strategy -- a method of location assignment that made sense with respect to the objects they were storing -- showed that having a preexisting system was tremendously helpful.

Now, if linear orders are insufficiently expressive, agents must rely on known systems of arrangement, or on some design that makes sense relative to the subject matter. For instance, in organizing icons in a MacIntosh style environment, it would not be surprising if users arranged their icons for `peripheral' equipment, such as hard and soft disks, printer, waste basket, fax machine, remote terminal, around the physical periphery of the screen, and in a way that would make sense if the screen were their office and the equipment distributed around the walls. The semantics is clear here. Hence it is relatively easy to remember where a given icon is to be found. But it is less easy to find a system that conveys what piece to take next that does not rely on some perceptual cue, such as next biggest, next in line. It is possible to make the system more complex by incorporating a procedure of choice, such as, if one needs a hex bolt, then use the one at the end of the hex bolt line, whereas if one needs a washer use the biggest washer that is left. But at some point, as the visual search involved in finding the next piece becomes more complex, the virtue of structuring items reduces.

	Figure 6. In many assembly tasks it is necessary to complete subassemblies before all parts can be put together. A simple trick some repair people use is to cluster subassemblies in groups, themselves possibly strictly ordered, and to arrange the groups in ways that reflect the global order of assembly. Here we see a subassembly represented by a depression in a simple linear ordering.

Case 5: Encoding Where to Place It

In assembly tasks we distinguished the selection problem from the placement problem. Arrangements that help solve the selection problem reduce the search space by encoding the property next piece to use in an easy to read off manner. Position in the spatial arrangement marks position in assembly sequence, so the simple heuristic: use the next piece, is a reliable guide to action. The fact that more expert agents can encode orderings in non-linear and not immediately obvious arrangements proves only that they operate with sophisticated categories, not that they cannot determine next in a trivial way.

It would be attractive if a simple, or tractable, arrangement could be found that solves both the selection and placement problems. For instance, one might try to place the pieces on the floor in a manner that reveals where they go in the growing assemblage, but in a way that also encodes next. Unfortunately there is more information than can be encoded naturally in two dimensions.

Consider the case of assembling a desk.

What should be apparent from this example is that as assemblages become more complicated it becomes harder to read next off the arrangement. This is not the same problem we discussed under non-linear orderings, above. The problem, now, is that if we lay out pieces in a way which encodes information about topological structure, we severely constrain the ways that remain for encoding sequence. As mentioned, it helps to have a systematic method of arranging items in mind beforehand. But, even so, the combinatorics are unbeatable. There is no escaping that complex topologies will evade description in 2D layouts, and no escaping that even with simple topologies there will be occasions when the next piece to assemble lies on the other side of the floor, with no obvious spatial reason for assuming it to be the next piece.

There are a few ways of viewing topological encodings. The most interesting, in my opinion, sees them as the data set for a simple assemblage program. Observe figure 7a. Suppose an agent is told 'fold each piece 90° and connect it with screws to the pieces it touches.' The layout on the floor is the data to this program. If the layout is properly set up, the three dimensional connectivity will follow as a consequence of applying the program. The agent needn't review mentally the results of applying the program, any more than he would in using a set of compasses to draw a circle. If certain background conditions are correct -- in the case of the compasses, that the paper is flat, in the case of the desk, that the layout folds correctly, then the algorithm will deliver the right answer given the data.

Now analytically a data set constitutes constraints on the output of a program. If the program is simple and the data set complex, the intelligence -- the constraint -- lies primarily in the data. This is the key idea behind logic programming. If, on the other hand, the data are simple and the program complex, the intelligence lies primarily in the program. This is the key idea behind standard procedural programming.

One technique expert assemblers learn is how to 'logic program' with the environment. They learn to put into the spatial arrangement enough information to use a simple procedure to complete the task. There is no reason this arrangement may not be planned out beforehand. Indeed it often is. But the point is that they can multiply the speed of on-line assembly if they lay out the parts well, and they can reduce the probability of an error.

	Figure 7. In figure a. we see a typical layout map for preparing the workspace to make assembly easy. The agent is advised to lay the parts down on the floor before the assembly begins. The physical layout serves as input to a simple assembly program. By contrast, in figure b. we see an alternative map that labels edges explicitly and explicitly states connectivity. Figuring out how to lay the assembly on the floor is itself a problem. So pieces tend to be labeled and stored in a pile. This leads to more visual search during assembly and more computation to ensure the right edges are connected. Not surprisingly, informal reports indicate that instructions that rely on matching numbers and edges prove to be harder in practice to follow.

Spatial Arrangements That Simplify Perception

In each of the examples just discussed the agent's decision problem was made combinatorially less complex by information that could be read off from the environment. One way or another, the amount of internal search required for choosing an action was reduced. A second fundamental way the problem of choosing an action can be simplified is by re-organizing arrangements to facilitate perception: to make it possible to notice properties or categories that were not noticed before, to make it easier to find relevant items, to make it easier for the visual system to track items.

Typically, in accounts of decision making, the cost of perception does not figure significantly in the combinatorics of choice. The cost of determining whether a perceptual operator applies to a world state or not, is assumed to have no effect on the size of the subgraph that must be searched, because search size is a function of the depth and breadth of a search, not how long it takes to identify a state, or test an operator. Hence, perceptual costs are treated as, at worst, contributing a constant increase in the complexity of a problem., they may increase the cost of a search from bd to a(bd).

In absolute time, as opposed to asymptotic time, however, if there is a way to more readily determine the action affordances at a choice point, or the applicability of a heuristic, the agent will have more time to make a choice. Any change which makes recognition faster certainly simplifies the psychological hardness of a problem.

Clustering To Categorize

Perhaps the most obvious way of simplifying perception is to arrange objects in space so that they form equivalence classes, or partitions, that reflect relevant preconditions, or properties that are useful to track, notice, or exploit. For instance, a standard precondition for washing a salad ingredient -- a tomato -- is that it not already have been washed. Clean and dirty tomatoes can be hard to tell apart. So one common ploy is to place washed tomatoes in one place, unwashed tomatoes in another. By segregating the two groups we highlight their differences. Examples of other objects already mentioned as being useful to classify include the side groups in the buffer region of checkout counters, scraps of wood in workshops, and playing cards which are usually ordered by suit and number in bridge, and by scoring category in gin rummy.

The primary value of such external partitioning is that it makes it easier:

Both factors are involved in recognizing the availability of actions and in monitoring the current state. If I can't find the garlic, I am not likely to think of rubbing it on the salad bowl -- I miss some available actions. And, if I can't tell whether the dishes are clean or dirty -- i.e. I fail to monitor correctly -- then I can't decide whether I should wash them.

Clustering helps solve these problems because it is harder to lose big things than little ones, and harder to miss seeing what a whole group is good for. For instance, memory for location, as was mentioned before, is regularly overestimated. It is harder to remember where a pen is, than its color. But if the pen is in a group of like colored objects, the sheer size of the colored group will simplify the visual search problem. Color can be used as both a memory aid and a visual cue.

A similar story holds for affordances. The fact that a group of heavy glass bottles is building up by the cash register highlights the fact that heavy items are available. As merchandisers well know, one way to increase the chance of being noticed is to occupy more space -- make bigger displays. The same method is used every day to simplify noticing affordances.

Other Techniques for Creating Categories

Clustering is only one of the ways agents have of creating equivalence classes on the fly. According to Gestalt theory other factors besides proximity which determine whether we perceive a set of items as a group are such things as how similar the items are (similarity), whether the items move together (common fate), whether they fit into a smooth, continuous line (good continuation), whether they can be seen as a closed form, and whether they stand out together against a background (surroundedness). We have already seen examples of several of these. Good continuation, for instance, is relied on by assemblers to distinguish parts in their assembly plan from random parts in the workshop. Similarity is used by baggers working in tight spaces where large heavy items, though clustered, are directly beside small items. An example of surroundedness was supplied by one reviewer of this paper. He mentioned that his father taught him to place the various pieces of his dismantled bicycle, many of which were small, on a sheet of newspaper. The newspaper served to mark out a region that was to be treated as special; it demarcated a boundary within which items of a particular sort were to be placed. Hence, it was easy to locate them, and they were less likely to be kicked about.

The idea of creating a special region applies not only to cases where there is a visible frame, a newspaper for instance, but to notional regions that an agent sets aside. By creating such regions it is sometimes possible to achieve tasks which might otherwise be impossible. An interesting example can be found, once again, in the blocks world.

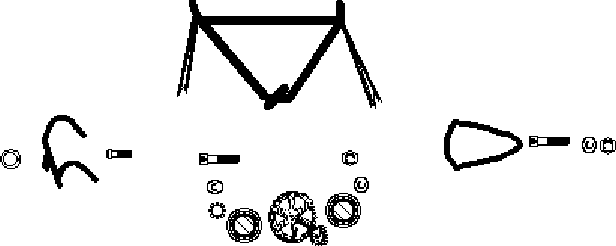
In (Chapman 91), David Chapman argued that it is possible to use a Pengi-like system to build a nine block tower -- spelling FRUITCAKE -- from an environment of 45 blocks strewn about, provided that nine of those blocks already spell fruitcake and so can serve as an example tower to copy. The technique his system uses requires having snapshots of the entire environment, and moving markers around these snapshots to make it possible to keep track of where the next useful block is, which blocks must be removed to free that useful block, and so on. Using these markers as a way of recording state information it is possible to rely on a simple compiled rule system to copy the goal stack.

To scale this system up to cope with constructing arbitrary goal towers, however, requires adding additional markers: one set to mark towers that have been successfully built; and a second set to mark the goal towers already built. If we did not have these extra markers, then, there would be nothing to stop the system from cannibalizing target towers for their parts, and nothing to stop the system from repeatedly copying goal towers. See fig 8a. Since there is considerable cost in maintaining large numbers of markers this is an unattractive solution. But, it is not the only solution. If we allow regionalizing the environment, and building knowledge of where those regions are into the system, we can build arbitrary numbers of towers using just the original markers.

The trick is to divide the workplace into regions for storing the goal stacks, for foraging for blocks, and for building the target stacks, and to create a known ordering within those. Thus, region 1 will contain the original goal stacks organized in the order they are to be built; region 2 will contain the blocks currently available for building towers, possibly organized alphabetically, but that is not necessary; and region 3 will contain the new stacks currently being built. A pengi-like system will now work successfully as long as we add three more rules. As soon as the current goal stack is completed, move to the next stack on the right in the goal stack region; if there is no goal stack to the right, announce success. Build target stacks in the target stack region, starting from the left and moving right. Search for blocks only in the resource region. As can be seen in Figure 8b. this is a simple way of preventing cannibalism, duplication, and failure to halt. The point, to repeat, is that by creating external regions it is possible to keep memory demands within psychologically realistic limits.

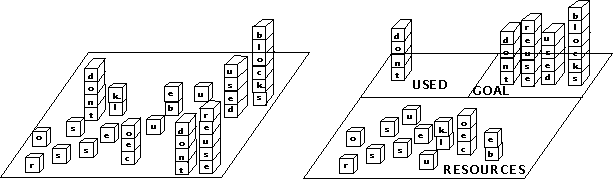	Figure 8. In figure A. we see a typical blocks world situation facing Blockhead, a Pengi-like tower copier. In order to reliably copy the goal stack, shown on the right, Blockhead must rely on five visual markers to keep track of the stack to copy, the block to copy, the current spot in the stack being cleared, the target block to be freed by clearing, as well as the stack being built. To copy more goal stacks would require more visual markers. In figure B, we see the space regionalized into a goal stack region, a block foraging region, and a target stack region. Stacks in the goal and target regions are ordered from left to right. If Blockhead knows about these regions it can copy an arbitrary number of stacks without relying on more visual markers.

Symbolic Marking

Yet another technique for categorizing, or identifying an object is to mark the object with a cue that draws attention, or prods recall. For instance, when there is a pair of hard to distinguish items we wish to differentiate, such as two wooden spoons -- one used for stirring a dark curry (currently cooking on the left front burner), the other for stirring a brown sauce (currently on the right front burner) -- we may mark their difference by associating them with a known distinguisher. For instance, we might keep them on the lids of their respective saucepans (particularly if those are different sizes), or we may place them beside one of the key ingredients (e.g. the curry tin). These are examples of symbolic positioning, or marking.

We have found marking to be an important resource for helping agents monitor task state. Here is an another example.

Markers are a form of reminder. But with a twist. Whereas perfect reminders both signal that something is to be remembered and encode what that something is, markers really only serve the first function: they signal that there is something here to notice or remember, but not what that is. For a marker to be effective it must serve as an easy to use cue for recall. The knife's thoughtful positioning, particularly if regularly so used, can provide the context for recall.

Clustering To Sharpen Perceptual Acuity

So far we have considered how clustering and thoughtful placement can highlight the category, or identity, of an item. By making more explicit the category of an item, agents can more readily perceptually track the functionally important elements in their environment. Few tasks make this more evident than solving jig saw puzzles.

At first this may seem just another case of clustering to produce equivalence classes. But more is going on here In solving a jig saw puzzle the recurrent problem is to identify, from among a large set of pieces, the single one which correctly fits the target space. One of the properties of the game that makes it hard is that both coarse and fine discriminations are necessary. Coarse discriminations help with planning. 'Cluster corner pieces! Look for parts of the sky!' But fine discriminations are necessary to determine exactly which individual piece will fit. Surprisingly, coarse grouping helps with noticing fine discriminations too.

The general strategy at work here is again a form of informational structuring. It is easier for an agent to narrow the search to the correct piece within a coarse group than to look for the piece from scratch. If the agent can create a hierarchical classification, visual search can be reduced from O(N) to O(log N). Hence coarse grouping is a useful pre-processing technique.

Even more interestingly, a clever grouping can actually increase the fineness of distinctions the agent is capable of noticing. I call this the vernier effect. Vernier discrimination in visual perception refers to the eye's ability to distinguish very small displacements in the alignment of two objects or lines. This capacity to tell whether two lines are lined up or displaced is harnessed in vernier scales. See figure 4. In classification, a similar effect occurs. When a jig saw piece is buried among a variety of rather differently shaped pieces, subjects pick it out on the basis of coarse differences. If it is buried among similar shaped pieces, subjects must pick it out on the basis of fine differences. These fine differences are noticeable precisely because we can lock in visually on subtle differences. Two objects that are otherwise indistinguishable can often be distinguished if their images can be superimposed. Proximity helps. So does quantity, for we thereby create a reference class for comparison which highlights the kind of differences to note. We change the resolution of our classification.

	Figure 9. A vernier is an auxiliary scale that slides along the divisions of a graduated instrument to indicate fractions of the divisions of the larger scale. It allows a user to make finer distinctions than possible with one scale alone. The perceptual principle verniers rely on is called vernier discrimination, which is the capacity of the eye to note when two lines are not perfectly aligned.

Saving Internal Computation

We have considered how spatial arrangements can reduce the amount of mental search involved in choice, and also reduce the amount of visual computation necessary to monitor current state, notice hints, and search for wanted items. A third way an embodied agent can enlist the world is to pass off computation. Familiar examples of such offloading show up in analog computations. When the tallest spaghetti noodle is singled out from its neighbors by striking the bundle on a table, a sort computation is performed by using the material and spatial properties of the world. An agent who encodes size or rank in noodle length, can compute a fast sort by means of this physical process, as long as the result can be decoded quickly. The method does not involve symbolic computation, or an item by item comparison. It works by creating a visual cue that serves to make the property in question explicit.

Such computational exploitations of the world are more common then usually realized. When a tailor flips over a paper cutout, he is effectively computing a description of the mirror image of the original shape. It is not evident that such exploitation of the world qualifies as `using space' intelligently. But I shall include a discussion of some of the issues because the line between using the world, and using the spatial properties of the world, is not an easy one to draw.

Let us turn now to an example that shows that the mental use of the world can occur even at high speed.

High Speed Offloading

We have found in our laboratory studies of a fast paced computer game, Tetris, see figure 10, that players will physically manipulate forms to save themselves mental effort.(Kirsh and Maglio 93) They modify the environment to cue recall, to speed up identification, and to generate mental images faster than they could if unaided. In short, they make changes to the world to save themselves costly and potentially error prone computations in the head.

	Figure 10. In Tetris, pieces enter the board from the top and the player has to decide whether to move them right, left or to rotate them. We have found that there is a burst of rotational activity in a region about 800 ms to 1800 ms when the player is working out where to place the piece. External rotation can be as fast as 150 ms, whereas internal rotation takes five to ten times as long.

The trick, in every case, is to modify visual input at exactly the right time to supply information needed by other computations. This is a version of just in time inventory control, only here, the inventory is informational. The effect is a highly interactional computation, where the information for a step in the computation is sometimes provided internally, and sometimes the information is provided externally. What binds the two together into a tightly coupled system is their timing. See figure 11 for a sketch of the kind of process model this suggests.

To take one example from Tetris, we found that about 800 to 1000 ms after a zoid enters the screen, players display a burst of rotations. See figure 10 for an explanation of Tetris. One hypothesis is that they rotate the piece rapidly to generate the mental icons they need to try out candidate placements. To rotate a zoid in the world takes far less time than to rotate its mental image. From our own studies we have determined that mental rotation of tetrazoids takes between 1000 and 1800 ms; physical rotation can take place in 200 ms. (Kirsh and Maglio, ibid.). By shifting the burden of imagery formation away from the mental rotation component, and giving it, instead, to the faster working motor and perceptual systems, an agent can save hundreds of milliseconds. This is what is meant by saying the agent uses the world to save internal computation. External rotation solves the problem 'what would this zoid look like if rotated 90 degrees?' Thus if there is a generate and test process occurring in players when they are trying to decide where to place a piece, a call to the motor system to physical rotate a piece can supply the generator with exactly what it needs. Computational steps are not actually eliminated; they are offloaded from the agent to the world.

	Figure 11. In this figure internal processing components are nudged forward in their own computations by inputs caused by the agent's actions. The difference between this and standard cascade models of processing is that internal modules here can request motor output without much mediation, causing changes in the external environment that are specifically targeted at improving their own performance. From (Kirsh and Maglio, forthcoming).

Externalizing Representations and Perspective Flipping

In high speed interactions, the agent and environment can be so tightly coupled that it may be plausible to view the two as forming a single computational system. In that case, some elements of the computation are outside the agent, some are inside, and the computation itself consists in the dynamic interaction between the two. The general idea that the dynamic relations holding being an embodied agent and its environment form a computational system has been advanced by Ed Hutchins and Sylvia Scribner. [Hutchins in press (a), (b); Scribner 86].

One fact about human cognition that lends itself to such interpretation is that there are important psychological differences between external and internal representations. In (Chambers and Reisberg 85) subjects were asked to form mental images of classically ambiguous figures, such as the Necker cube, the duck/rabbit. They had been shown several different ambiguous images, and understood the relevant notion of ambiguity, although importantly, they were naive to the test figures. Chambers and Reisberg found that none of the subjects could discover any ambiguity in their images. Evidently, internal representations, unlike their external counterparts, seem to come with their interpretation fixed. An agent conjuring an image cannot separate the interpretation of the image from the image itself. Reisberg (87) had this to say:

The implication is that if we want to discover important new elements in a structure, particularly if this requires looking for novel interpretations, we are better off depicting it externally, or consulting some pre-existing external representation of it. The skills we have developed for dealing with the external world go beyond those we have for dealing with the internal world. Hence, the reason creative activity tends to make such extensive use of external representations may be because, in the discovery phase, one wants to note as many possible extensions and variations to ones ideas as possible. This is easier if the representations are externalized.

Now, because computation regularly involves generate and test phases it is possible that the most intelligent use of space is to try out conjectures. For example, in the game of scrabble, when we are searching for words, it is customary to shuffle tiles around in the hope of triggering an association. We may call activity of this sort, self cueing.

The principle of self cueing is a type of externalization that depends for its success on two factors: an internal module whose operations are, more or less, encapsulated from interference by other modules, and a tight coupling between internal and external processes. There would be no point fiddling with the outside world to jog our memories if we could do the same internally just as fast. The extra value flows from the way we associate items. We can get a fresh way of looking at our scrabble tiles, if we shuffle them. This approach crops up in a range of self-help techniques. To solve an algebra problem we make explicit many of the obvious transformations. To solve a geometry problem we often draw a figure, or introduce constructions that alter the appearance of the structure. A theory of how externalization improves cognition would certainly go beyond ways of using spatial arrangements. But, we can be certain that in any such theory, more than lip service will be paid to the role of spatial arrangement.

Conclusion

Throughout this paper, I have presented ways agents have of managing the spatial arrangements of items in their workplace. To make it easier to stay in control of activity, we rely on techniques which reduce the memory load of tasks, the amount of internal computation necessary, or which simplify the visual search and categorization that is inevitably involved in performance. Some of these techniques we consciously apply, some we apply unwittingly. But all reflect our tight coupling to the world. A coupling becomes tight, when timing becomes important. In Tetris, for instance, zoids are rotated in the world to save mental rotation. Timing is crucial. A few hundred milliseconds later, and a given rotation will fail to carry useful information for a player. In bagging groceries, or in cooking, we place items around us at particular moments. If well timed, such placements serve to remind us, to cue attention, to prevent us from considering irrelevant alternatives. The virtue of such cues and constraints is that they structure the information we take in as input. In fast paced environments, this informational structuring supplies hints and clues that advance computations that are in progress. In slower paced environments, such as scrabble, jig saw puzzle playing, and shelving books, informational structuring also helps supply ideas, hints and distinctions that facilitate problem solving. Even though slower paced tasks involve choices that spans tens of seconds, it is still important to have the right information at the right time. It is amazing how prevalent such phenomena are in our everyday activities.

One theme which has been recurring, but which I have left largely unexamined, is that many of our structuring actions serve to reduce the descriptive complexity of our environments. This makes it easier to track the state of the environment. The idea first surfaced in our discussion of the advantage of organizing lettered blocks alphabetically, or into known chunks, such as morphemes. A planner who first arranges blocks alphabetically reduces the need for visual search because he or she is able to describe the state of the environment more compactly. The position of a block in an alphabetical list is known by heart, so it can be generated without further knowledge of the particulars of the environment. The same applies if we organize blocks into well known units, given an environment in which the letters TEOEPPAPTTASSCERLAEP appear, we put such as ; we put a much smaller strain on Working Memory if we manage the environment so that the stimulus we see is chunked as in PET TAPE APPLE SOCRATES. Preprocessing the world saves processing the representation of the world. Put another way, the greater our understanding of the organization we maintain outside, the less we have to memorize.

It is in this spirit of reducing the descriptive complexity of the environment, that we can understand the virtue of creating critical cues, such as the relative length cue created by the cook who lined up the vegetables, described in the introduction. When a cue is both easy to monitor, and it carries all the information the agent need to know about the state of the ongoing process, it reduces the processing required to track the current state of the environment. It reduces the descriptive complexity of that state to a few bits.

A tabular summary of some of the examples discussed in the text follows. These cases span only a fraction of the range of intelligent uses of space in everyday life, but I believe they are representative.

Theorists in AI have dwelled on the intelligent use of time, hardly considering space. Yet vision, our primary spatial sense, is one of humanity's most powerful capacities. It is little wonder that diagrams facilitate problem solving. Should we not expect much of our everyday competence might come from informationally structuring our workspace? I have tried to show what, in certain cases, this might mean, and why it is a reasonable idea to develop.

References

Agre, P. (forthcoming) The Dynamics of Everyday Life, Cambridge, UK: Cambridge Univ. Press.

Agre, P. Hassles, MIT working paper, Cambridge Mass.

Agre, P. & Chapman, D. (1987). Pengi: An implementation of a theory of activity. In Proceedings of the Sixth National Conference on Artificial Intelligence, pp196-201.

Agre, P. & Horswill, I. (1992). Cultural Support for Improvisation. In Proceedings of the Eleventh National Conference on Artificial Intelligence pp.

Beach, K. (1985). Learning to become a bartender: The role of external memory cues at work. Paper presented at Eastern Psychological Association, Boston, MA.

Brooks, R. (1991) Intelligence without Representation, Artificial Intelligence, 47, 141-160.

Chapman, D. (1991) Penguins can make cake, AI Magazine.

Chase, W. G. & Simon, H. A. (1973). Perception in Chess. Cognitive Psychology, 4, 55-81.

Chambers, D. and Reisberg, D. (1985). Can mental images be ambiguous? Journal of Experimental Psychology: Human Perception and Performance. 11, 317-328.

Charness, N. (1981). Search in chess: Age and skill differences. Journal of Experimental Psychology: Human Perception & Performance, 7, 467-476.

Cleveland, W.S. & McGill, R. (1985). Graphical perception and graphical methods for analyzing scientific data. Science, 229, 828-833.

Cohen, G. (1989). Memory in the Real World, Hillsdale,NJ: Lawrence Erlbaum Associates

de la Rocha, O. (1985). The reorganization of arithmetic practice in the kitchen. Anthropology and Education Quarterly. 16, 193-198.

Elster, J. (1982). Ulysses and the Sirens, Studies in Rationality and Irrationality. Cambridge: Cambridge Univ. Press.

Gibson, J.J. (1977). The theory of affordances. In R.E. Shaw & J. Bransford (Eds.), Perceiving, acting, and knowing. Hillsdale,NJ: Lawrence Erlbaum Associates

Goodnow, J.J. (1986). Some lifelong everyday forms of intelligent behavior: organizing and reorganizing, in Sternberg, R J. & R. K. Wagner, (eds.) Practical Intelligence: Nature and origins of Competence in the everyday world, Cambridge Univ. Press, Cambridge. PP 143-162.

Greeno, J. G., (1989). Situations, Mental Models, and Generative Knowledge, in Klahr D, & K. Kotovsky, (eds.) Complex Information Processing, Hillsdale N.J. Lawrence Erlbaum Associates, pp. 285-318.

Hutchins, E. (in press a). How a Cockpit remembers its speeds. Cognitive Science.

Hutchins, E. (in press b). Cognition in the Wild. Cambridge,MA: MIT Press.

Kamman, M. (1982) The making of a Chef. New York, NY: Atheneum.

Kirsh, D. (1991a). When in Information Explicitly Represented? In (ed.) P. Hanson, Information, Language and Cognition. Oxford University Press, Oxford, pp. 340-365.

Kirsh, D. (1991b) Today the earwig, tomorrow man? Artificial Intelligence 47, 161-184.

Kirsh, D. & Maglio, P. (1992). Some Epistemic Benefits of Action: Tetris, A Case Study, in Proceedings of the fourteenth Annual Cognitive Science Society, Morgan Kaufman

Kirsh D. & Maglio, P. (in press). On Distinguishing Epistemic from Pragmatic Actions, Cognitive Science.

Kotovsky, K & Fallside, D. (1989), Representation and Transfer in Problem Solving, in Klahr D, & K. Kotovsky, (eds.) Complex Information Processing, Hillsdale N.J. Lawrence Erlbaum Associates, pp. 69-108

Lansdale, M.(1991) Remembering about Documents: memory for appearance, format, and location. Ergonomics, 34.-8, 1161-1178.

Lansdale, M. & E. Edmonds, (1992). Using memory for events in the design of personal filing systems, International Journal of Man-Machine Studies, pp. 97-126.

Larkin J. H. (1989), Display-Based Problem Solving, in Klahr D, & K. Kotovsky, (eds.) Complex Information Processing, Hillsdale N.J. Lawrence Erlbaum Associates,. pp. 319-342.

Larkin J. H. & H. Simon, (1987). Why a Diagram is (Sometimes) Worth Ten Thousand Words, Cognitive Science, 11, 65-99.

Lave, J. (1988). Cognition in Practice. Cambridge: Cambridge Univ. Press.

Lave, J. (1977). Cognitive Consequences of traditional apprenticeship training in West Africa. Anthropology and Education Quarterly. 8(3), 177-180.

Malone, T. W. (1983), How do people organize their desks? Implications for the design of office automation systems, ACM Transactions on Office Systems, 11, 99-112.

Norman D.A. (1981), Categorization of Action Slips. Psychological Review, 88, 1-15.

Norman D.A. (1988). The Psychology of Everyday Things. New York: Basic Books.

Rasmussen, J. (1986). Information Processing and Human-Machine Interaction. Amsterdam: North Holland.

Rasmussen, J. (1980) What can be learned from human error reports? In K. Duncan, M. Gruneberg & D. Wallis (Eds.), Changes in Working Life. London: Wiley.

Reason J. T.(1990), Human Error, Cambridge: Cambridge Univ. Press. 1990.

Reason J. T & K. Mycielska.(1982). Absent-Minded? The psychology of Mental Lapses in Everyday Errors. Englewood Cliffs: N.J.: Prentice Hall.

Riesberg D., (1987), External Representations and the Advantages of Externalizing One's Thoughts, Proceedings of the Ninth Annual Cognitive Science Society. Morgan Kaufman

Rouse, W.B. (1981). Models of Human Problem Solving: Detection, diagnosis and compensation for system failures. Proceedings of IFAC Conference on Analysis, Design and Evaluation of Man-Machine Systems.

Savage J. E. (1976) The Complexity of Computing, John Wiley and Sons, New York.

Scribner S., 1986, Thinking in Action: some characteristics of practical thought, in Sternberg R J. & R. K. Wagner, (Eds.) Practical Intelligence: Nature and origins of Competence in the everyday world, Cambridge: Cambridge Univ. Press. pp. 13-30.

Simon, H. A. & Hayes, J. (1976). The understanding process: Problem Isomorphs. Cognitive Psychology, 8, 165-190.

Stevens, J. (1985) An observational study of skilled memory in waitresses. Paper presented at Eastern Psychological Association, Boston, MA.

Tarjan R. E. (1985,) Amortized Computational Complexity, SIAM J Comput 14, pp 306-318.